В позиционной системе счисления с целочисленным основанием q любое число можно записать в привычной нам свёрнутой форме или же в развёрнутой.
Число A, записанное в системе счисления с основанием q, будем записывать так: Aq (нижний индекс q показывает основание системы счисления).
Например:
- 123410 — число в десятичной системе счисления (q=10);
- 4567 — число в семеричной системе счисления (q=7);
- 10101012 — число в двоичной системе счисления (q=2).
В общем виде число, записанное в свёрнутом виде, мы можем представить в такой записи:
±a_{n-1}a_{n-2}...a_1a_0В этой записи:
- знак ± показывает знак числа (в дальнейшем для простоты будем рассматривать только положительные числа);
- n – количество разрядов числа;
- an-1 .. a0 — цифры числа, а нижние индексы — соответствующие порядковые номера (причём младший разряд имеет номер 0; очевидно, тогда старший будет иметь номер n–1).
Мы знаем, что привычные нам десятичные числа легко разложить на разряды. Так, число 123410 — тысяча двести тридцать четыре — буквально означает следующее: «одна тысяча, две сотни, три десятка и четыре единицы».
1234_{10} = 1 \cdot 1000 + 2\cdot100 + 3\cdot10 + 4 \cdot 1Нетрудно заметить, что вес каждого разряда — это степень десяти (а десять — основание системы счисления).
1234_{10} = 1 \cdot 1000 + 2\cdot100 + 3\cdot10 + 4 \cdot 1 = \newline
= 1\cdot10^3 + 2\cdot10^2+3\cdot10^1 + 4\cdot10^0При этом показатели степени, в которую возводятся основания системы счисления, соответствуют порядковым номерам разрядов. Нумеруем разряды по вышеописанному принципу: младший разряд — 0, старший — n-1.
Такую форму и называют развёрнутой формой записи числа.
Рассмотрим ещё один пример — число 6375.
В нём:
- цифра 6 стоит в третьем разряде (тысячи, 103),
- цифра 3 – во втором разряде (сотни, 102),
- цифра 7 – в первом (десятки, 101),
- цифра 5 – в нулевом (единицы, 100).
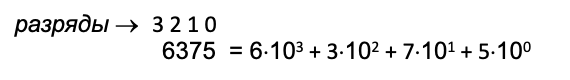
Правило:
Для того, чтобы представить число в развёрнутой форме, необходимо:
- Пронумеровать цифры (разряды) числа так, чтобы младший разряд целой части имел индекс 0, нумерация разрядов целой части возрастала (от 0 до n-1).
- Представить исходное число в виде суммы произведений цифры на основание системы счисления, возведённое в степень, равную позиции цифры.
В общем виде эту запись можно выразить формулой:
A_q = ± (a_{n-1}\cdot q^{n-1}+a_{n-2}\cdot q^{n-2} + ... + a_1\cdot q^1 + a_0\cdot q^0)Обратите внимание: любое число (кроме нуля), возведённое в нулевую степень, равно единице!
n^0 = 1
Ещё примеры:
123_{10} = 1\cdot10^2 + 2 \cdot10^1+3\cdot10^0 \newline
10110_{2} = 1\cdot2^4 + 0\cdot2^3+1\cdot2^2+1\cdot2^1+0\cdot2^0 \newline
1212_3 = 1\cdot3^3+2\cdot3^2+1\cdot3^1+2\cdot3^0 \newline
21456_7 = 2\cdot7^4+1\cdot7^3+ 4\cdot7^2+5\cdot7^1+6\cdot7^0Заметим, что если число, записанное в произвольной позиционной системе счисления, представить в развёрнутой форме, а затем произвести вычисления, мы получим десятичное число, эквивалентное исходному.
Иными словами, мы выполним перевод из произвольной системы счисления с основанием q в десятичную систему.
10110_{2} = 1\cdot2^4 + 0\cdot2^3+1\cdot2^2+1\cdot2^1+0\cdot2^0 = \newline
= 1\cdot16+0+1\cdot4+1\cdot2+0= 16 + 4 + 2 = 22_{10}Таким образом,
10110_2 = 22_{10}